I want to talk about a comonad that came up at work the other day. Actually, two of them, as the data structure in question is a comonad in at least two ways, and the issue that came up is related to the difference between those two comonads.

This post is sort of a continuation of the Comonad Tutorial, and we can call this “part 3”. I’m going to assume the reader has a basic familiarity with comonads.

Inductive Graphs

At work, we develop and use a Scala library called Quiver for working with graphs). In this library, a graph is a recursively defined immutable data structure. A graph, with node IDs of type V, node labels N, and edge labels E, is constructed in one of two ways. It can be empty:

1

def empty[V,N,E]: Graph[V,N,E]

Or it can be of the form c & g, where c is the context of one node of the graph and g is the rest of the graph with that node removed:

1
2
3
4
5
6
7
8

case class Context[V,N,E](
  inEdges: Vector[(E,V)],
  vertex: V,
  label: N,
  outEdges: Vector[(E,V)]
) {
  def &(g: Graph[V,N,E]): Graph[V,N,E] = ???
}

By the same token, we can decompose a graph on a particular node:

1
2
3
4

g: Graph[V,N,E]
v: V

g decomp v: Option[GDecomp[V,N,E]]

Where a GDecomp is a Context for the node v (if it exists in the graph) together with the rest of the graph:

1

case class GDecomp[V,N,E](ctx: Context[V,N,E], rest: Graph[V,N,E])

Recursive decomposition

Let’s say we start with a graph g, like this:

I’m using an undirected graph here for simplification. An undirected graph is one in which the edges don’t have a direction. In Quiver, this is represented as a graph where the “in” edges of each node are the same as its “out” edges.

If we decompose on the node a, we get a view of the graph from the perspective of a. That is, we’ll have a Context letting us look at the label, vertex ID, and edges to and from a, and we’ll also have the remainder of the graph, with the node a “broken off”:

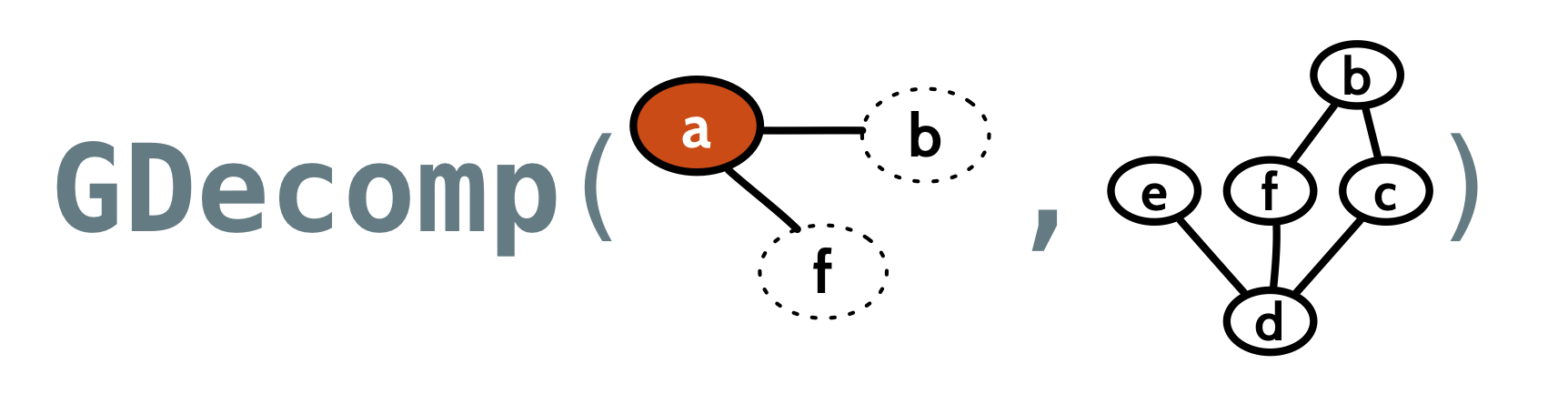
Quiver can arbitrarily choose a node for us, so we can look at the context of some “first” node:

1
2
3

g: Graph[V,N,E]

g.decompAny: Option[GDecomp[V,N,E]]

We can keep decomposing the remainder recursively, to perform an arbitrary calculation over the entire graph:

1
2
3
4

f: (Context[V,N,E], B) => B
b: B

(g fold b)(f): B

The implementation of fold will be something like:

1
2
3

g.decompAny map {
  case GDecomp(ctx, rest) => f(ctx, rest.fold(b)(f))
} getOrElse b

For instance, if we wanted to count the edges in the graph g, we could do:

1
2
3

(g fold 0) {
  case (Context(ins, _, _, outs), b) => ins.size + outs.size + b
}

The recursive decomposition will guarantee that our function doesn’t see any given edge more than once. For the graph g above, (g fold b)(f) would look something like this:

Graph Rotations

Let’s now say that we wanted to find the maximum degree of a graph. That is, find the highest number of edges to or from any node.

A first stab might be:

1
2
3
4
5

def maxDegree[V,N,E](g: Graph[V,N,E]): Int =
  g.fold(0) {
    case (Context(ins, _, _, outs), z) =>
      (ins.size + outs.size) max z
  }

But that would get the incorrect result. In our graph g above, the nodes b, d, and f have a degree of 3, but this fold would find the highest degree to be 2. The reason is that once our function gets to look at b, its edge to a has already been removed, and once it sees f, it has no edges left to look at.

This was the issue that came up at work. This behaviour of fold is both correct and useful, but it can be surprising. What we might expect is that instead of receiving successive decompositions, our function sees “all rotations” of the graph through the decomp operator:

That is, we often want to consider each node in the context of the entire graph we started with. In order to express that with fold, we have to decompose the original graph at each step:

1
2
3
4
5
6
7

def maxDegree[V,N,E](g: Graph[V,N,E]): Int =
  g.fold(0) { (c, z) =>
    g.decompose(c.vertex).map {
      case GDecomp(Context(ins, _, _, outs), _) =>
        ins.size + outs.size
    }.getOrElse(0) max z
  }

But what if we could have a combinator that labels each node with its context?

1

def contextGraph(g: Graph[V,N,E]): Graph[V,Context[V,N,E],E]

Visually, that looks something like this:

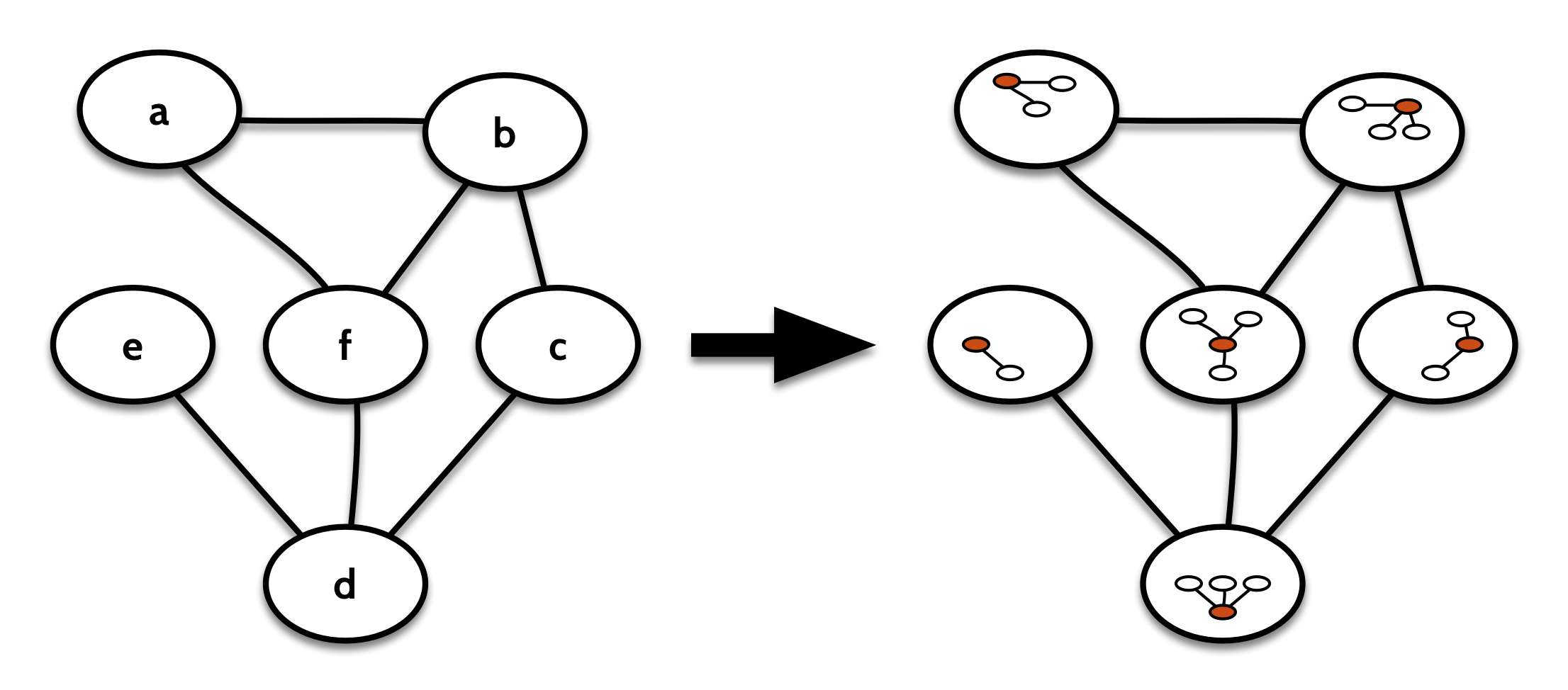
If we now fold over contextGraph(g) rather than g, we get to see the whole graph from the perspective of each node in turn. We can then write the maxDegree function like this:

1
2
3
4

def maxDegree[V,N,E](g: Graph[V,N,E]): Int =
  contextGraph(g).fold(0) { (c, z) =>
    z max (c.label.ins.size + c.label.outs.size)
  }

Two different comonads

This all sounds suspiciously like a comonad! Of course, Graph itself is not a comonad, but GDecomp definitely is. The counit just gets the label of the node that’s been decomped out:

1
2
3
4
5
6
7

def gdecompComonad[V,E] = new Comonad[λ[α => GDecomp[V,α,E]]] {

  def counit[A](g: GDecomp[V,A,E]): A = g.ctx.label

  def cobind[A,B](g: GDecomp[V,A,E])(
                  f: GDecomp[V,A,E] => B): GDecomp[B] = ???
}

The cobind can be implemented in one of two ways. There’s the “successive decompositions” version:

1
2
3
4
5
6
7

def cobind[A,B](g: GDecomp[V,A,E])(
                f: GDecomp[V,A,E] => B): GDecomp[B] =
  GDecomp(g.ctx.copy(label = f(g)),
          g.rest.decompAny.map {
            val GDecomp(c, r) = cobind(_)(f)
            c & r
          } getOrElse empty)

Visually, it looks like this:

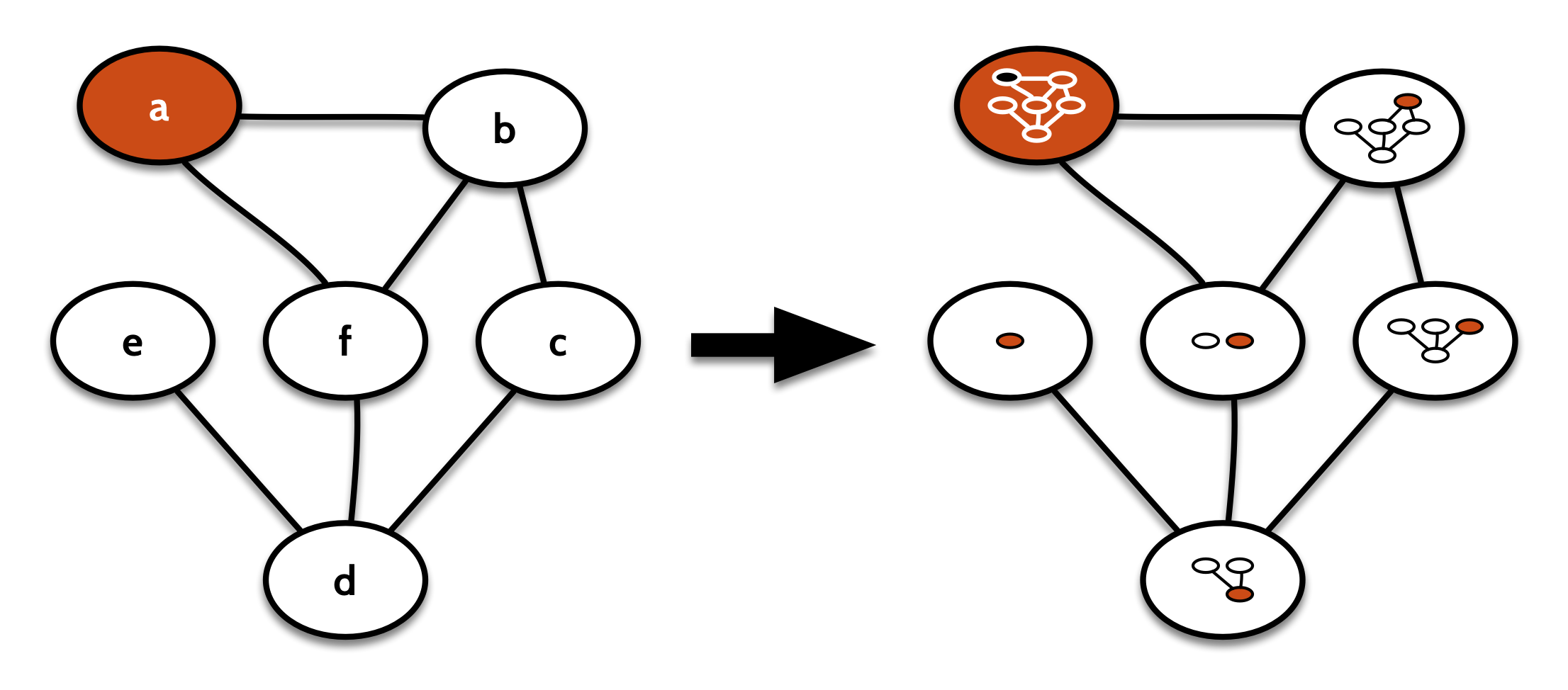
It exposes the substructure of the graph by storing it in the labels of the nodes. It’s very much like the familiar NonEmptyList comonad, which replaces each element in the list with the whole sublist from that element on.

So this is the comonad of recursive folds over a graph. Really its action is the same as as just fold. It takes a computation on one decomposition of the graph, and extends it to all sub-decompositions.

But there’s another, comonad that’s much more useful as a comonad. That’s the comonad that works like contextGraph from before, except instead of copying the context of a node into its label, we copy the whole decomposition; both the context and the remainder of the graph.

That one looks visually more like this:

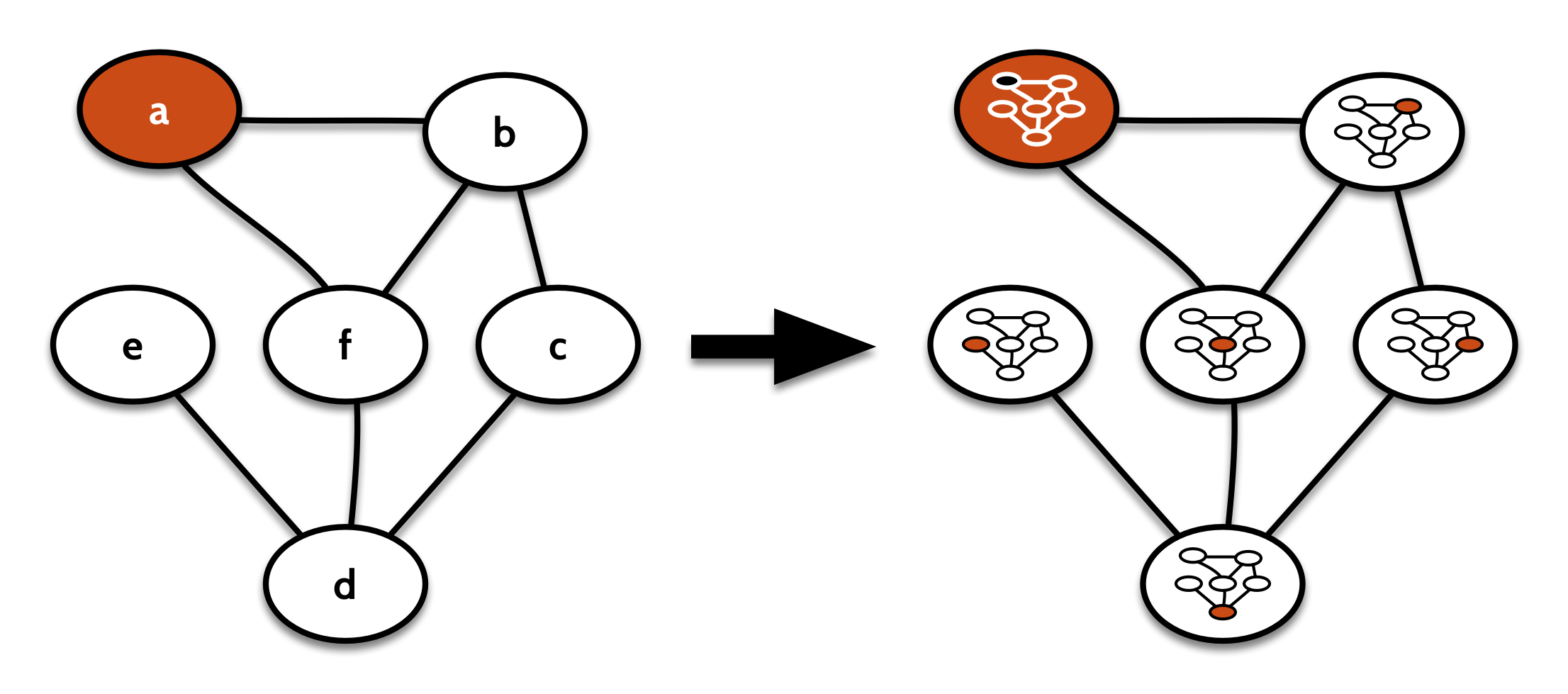
Its cobind takes a computation focused on one node of the graph (that is, on a GDecomp), repeats that for every other decomposition of the original graph in turn, and stores the results in the respective node labels:

1
2
3
4
5
6
7
8

def cobind[A,B](g: GDecomp[V,A,E])(
                f: GDecomp[V,A,E] => B): GDecomp[B] = {
  val orig = g.ctx & g.rest
  GDecomp(g.ctx.copy(label = f(g)),
          rest.fold(empty) { (c, acc) =>
            c.copy(label = f(orig.decomp(c.vertex).get)) & acc
          })
}

This is useful for algorithms where we want to label every node with some information computed from its neighborhood. For example, some clustering algorithms start by assigning each node its own cluster, then repeatedly joining nodes to the most popular cluster in their immediate neighborhood, until a fixed point is reached.

As a simpler example, we could take the average value for the labels of neighboring nodes, to apply something like a low-pass filter to the whole graph:

1
2
3
4
5
6
7

def lopass[V,E](g: Graph[V,Int,E]): Graph[V,Int,E] =
  g.decompAny.map { d => cobind(d) { x =>
    val neighbors = (x.inEdges ++ x.outEdges).map { n =>
      g.decomp(n).get.ctx.label
    }
    (neighbors.sum + x.label) / (neighbors.length + 1)
  }} getOrElse g

The difference between these two comonad instances is essentially the same as the difference between NonEmptyList and the nonempty list Zipper.

It’s this latter “decomp zipper” comonad that I decided to ultimately include as the Comonad instance for quiver.GDecomp.